一维相位去包裹:原理与仿真
一维相位去包裹:原理与仿真
Off-Topic
未觉池塘春草色,阶前梧叶已秋声。
-–—朱熹
时光飞逝,转眼就要毕业了。前天导师打电话摧我,这几个月就毕业了,你那毕业设计得赶紧做了。想想真是,四年倏忽过去,浑然不觉,已近毕业。
也许这是最后自在平静的日子了,时间却像沙子,越用力抓紧,从指间溜走地越快。
两年过得太快,I follow my passion,做了太多没用的事,有得有失。只是希望:
You can't connect the dots looking forward you can only connect them looking backwards. So you have to trust that the dots will somehow connect in your future. You have to trust in something: your gut, destiny, life, karma, whatever. Because believing that the dots will connect down the road will give you the confidence to follow your heart, even when it leads you off the well worn path.
-–—Steve Jobs, Stanford Commencement Adress, 2005
为何相位重要
我大学的专业是光学,时至今日,依然清晰记得两年前在阴暗的实验室做全息摄像的实验。我们几个同学花了好久把光路摆好,让激光打在物体上反光到干版上曝光。然后拿到什么试剂中定形。最后在拿出来用激光将物体的影响重新清晰的放出三维的像时,心里相当兴奋。
为什么全息照相能产生立体的像呢?普通的照相技术都是仅仅记录光波的强度,而不记录相位,因此失去了很多相位中的信息。但全息照相通过相干光(激光)之间的干涉在干版上同时记录下了强度和相位,再用相干光照射干版重放,好像光是从真的物体发出的一样。
如果您也做过这种实验,您应该知道为什么相位重要了。
这还有另一个例子,关于爱因斯坦和蒙娜丽莎。
我从《Two Dimensional Phase Unwrapping Theory Algorithms and Software》中看到了这个例子,然后自己动手用python试了试。
以下代码用来交换两个图片的相位
# -*- coding: utf-8 -*- # <nbformat>3.0</nbformat> # <codecell> from scipy.fftpack import * # <codecell> # read file im_1 = plt.imread('einstein.jpg') im_2 = plt.imread('monalisa.jpg') # fft and reverse two images' phase m_1, p_1 = np.abs(fft2(im_1)), np.angle(fft2(im_1)) m_2, p_2 = np.abs(fft2(im_2)), np.angle(fft2(im_2)) # <codecell> im_swapphase_1 = np.real(ifft2(m_1 * np.cos(p_2) + m_1 * np.sin(p_2) * 1j)) im_swapphase_2 = np.real(ifft2(m_2 * np.cos(p_1) + m_2 * np.sin(p_1) * 1j)) # <codecell> plt.figsize(10,10) plt.gray() plt.subplot(2,2,1) plt.imshow(im_1, origin='lower') plt.subplot(2,2,2) plt.imshow(im_2, origin='lower') plt.subplot(2,2,3) plt.imshow(im_swapphase_1, origin='lower') plt.subplot(2,2,4) plt.imshow(im_swapphase_2, origin='lower')
上面两幅图是交换相位前的图,下面两幅是之后的。显然,一团糟,相位中是有信息的。

为何要相位去包裹
简单地说,就是说,任何仪器,比如说量角器,顶多只能测得(\(-\pi, \pi\)]之间的量,但真正的相位角度不该这样,而是分布在实数空间内,应该是测得的(\(-\pi, \pi\)]之间的值的2$π$整数倍。
真正的相位值被“包裹”起来了,但为什么要解包裹呢?
不解包裹无法对相位进行计算。
Itoh的路径积分法
我们先定义一个获取包裹相位的算子\(\mathscr{W}\),该算子将相位包裹,获取位于$(-π,π]$之间的包裹相位。
\[\mathscr{W}\varphi = \arctan[\cos(Real \varphi / Img \varphi)]\]
还可以这样写
\[\mathscr{W}\{\varphi(n)\} = \psi(n) = \varphi(n) + 2\pi k(n)\]
其中$k(n)$是使包裹相位位于$-π,π$之间的值。
显然包裹相位$ψ(n)$有:
\[\pi \geq \psi(n) \gt -\pi\]
定义差分算子$Δ$:
\[\Delta \{\varphi(n)\} = \varphi(n+1) - \varphi(n)\]
\[\Delta \{k(n)\} = k(n+1) - k(n)\]
计算被包裹相位的差分:
\[\Delta \{\psi(n)\} = \Delta \{\varphi(n)\} + 2\pi\Delta \{k_1(n)\}\]
我们再用$\mathscr{W}$作用于该差分得:
\[\mathscr{W}\{\Delta \{\psi(n)\}\} = \Delta \{\varphi(n)\} + 2\pi[\Delta \{k_1(n)\} + k_2(n)]\]
显然上式结果应该位于\((-\pi,\pi]\),假如此时还有$Δ \{ϕ(n)\}\(也位于\)(-π,π]$,则上式右边第二项$2π[Δ \{k\1(n) \} + k2(n)]$应该为零,则有:
\[\Delta \{\varphi(n)\} = \mathscr{W}\{\Delta \{\psi(n)\}\} \]
显然,由该差分式可得:
\[\varphi(m) = \varphi(0) + \sum_{n=0}^{m-1} \mathscr{W}\{\Delta \{\mathscr{W}\{\varphi(n)\}\}\} \]
上式说明,真实相位可以通过对包裹相位的差分的包裹进行积分求得。
于是itoh的一维相位去包裹算法综述如下:
对信号相位数组\(\psi(i),0 \leq i \leq N-1\)
- 计算相位差分\(D(i) = \psi(i+1)-\psi(i), i=0,\ldots,N-2\)
- 计算包裹的相位差分\(\Delta(i) = \Delta\{D(i)\}, i=0,\ldots,N-2\)
- 初始化初值\(\varphi(0)= \psi(0)\)
- 累加解包裹\(\varphi(i) = \psi(i) + \Delta(i)\)
Itoh的方法很简单实用,但受到两个重要因素的影响:相位失真和噪声。下面仿真两种情况的影响。
仿真
对正弦波相位函数(间谐波,一切波的基础)
\[\varphi(t) = 10\sin(10t), 0 \leq t \leq 1\]
通过计算可以得知,使之不产生相位失真,区间内至少有32个采样点:
对相位变化有
\[\Delta \varphi = \dot{\varphi}\Delta t\]
其中 \(\dot{\varphi} = d\varphi / dt = 100\cos10t\) ,可看出相位在 \(n\pi/10\) 取得极值,加上条件:
\[\left\vert\Delta \varphi\right\vert \lt \pi\]
则
\[\left\vert \frac{100}{N} \cos 10t \right\vert \lt \pi\]
得
\[N \gt 31.83\]
则对这个函数如果采样率低于32就会产生相位失真。
# -*- coding: utf-8 -*- # <nbformat>3.0</nbformat> # <codecell> import numpy as np import matplotlib.pyplot as plt # <codecell> # phase function def pf(x): return 10 * np.sin(10 * x) # wrap function def wrap(x): return np.arctan2(np.sin(x), np.cos(x)) # unwrap function def wrap_diff(x): return wrap(np.diff(x)) def unwrap(x): y = x y[0] = x[0] for i in range(len(x) - 1): i += 1 y[i] = y[i - 1] + wrap_diff(x)[i - 1] return np.array(y) def noise(x, snr): return x + np.random.normal(loc=0.0, scale = np.sqrt(np.max(x) / 2 ** snr), size=len(x)) def show_unwrap(x,y,y_w,t,p): plt.ylim((-12,12)) plt.ylabel("Phase in Radians") p_w, = plt.plot(x, y_w,'o:') p_o, = plt.plot(t,p,':') p_u, = plt.plot(x,y,'s') plt.legend([p_w, p_o, p_u], ["sampled wrapped phase", "original phase function", "unwrapped phase"]) # <headingcell level=1> # 当取样点为num时 # <codecell> # Origin t = np.arange(0,1,0.01) p = pf(t) # plot ## num 50 plt.subplot(311) plt.title("num = 50") # sampled data num = 50 x = np.linspace(0,1,num) # wrapped phase y_w = wrap(pf(x)) # unwrapped wraped phase y = unwrap(wrap(pf(x))) show_unwrap(x, y, y_w, t, p) ## num = 32 plt.subplot(312) plt.title("num = 32") # sampled data num = 32 x = np.linspace(0,1,num) # wrapped phase y_w = wrap(pf(x)) # unwrapped wraped phase y = unwrap(wrap(pf(x))) show_unwrap(x, y, y_w, t, p) ## num = 31 plt.subplot(313) plt.title("num = 31") # sampled data num = 31 x = np.linspace(0,1,num) # wrapped phase y_w = wrap(pf(x)) # unwrapped wraped phase y = unwrap(wrap(pf(x))) show_unwrap(x, y, y_w, t, p) plt.xlabel("Relative Time") # <headingcell level=1> # 噪声 # <codecell> # noise influence x = np.linspace(0,1,200) y = pf(x) y_10 = unwrap(wrap(noise(y,10))) + 20 y_5 = unwrap(noise(wrap(y), 5)) + 40 y_2 = unwrap(noise(wrap(y), 2)) + 60 y_1 = unwrap(noise(wrap(y), 1)) + 80 # plot plt.xlabel("Relative Time") plt.ylabel("Phase in Radians") p_o, = plt.plot(t,p) p_1, = plt.plot(x,y_1,'--') p_2, = plt.plot(x,y_2,'-.') p_5, = plt.plot(x,y_5,':') p_10, = plt.plot(x,y_10,':') plt.legend([p_o, p_1, p_2, p_5, p_10], ["Origin", "SNR=1", "SNR=2", "SNR=5", "SNR=10"]) # <codecell>
我们可以看到:
-
在采样率低于某一关键值32时基本没法解出正确相位。
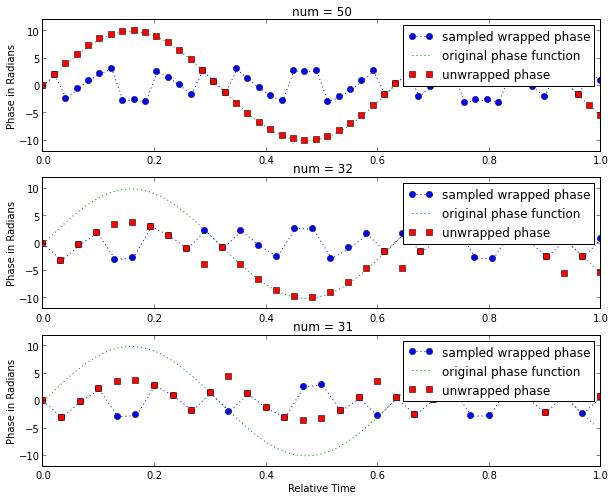
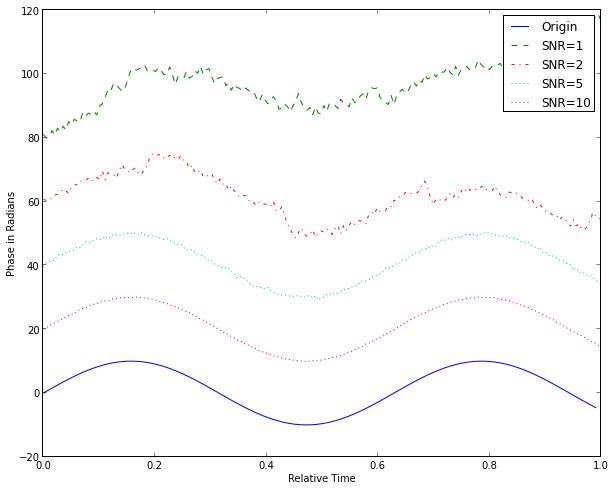
- 信噪比越低,解包裹效果越差。
Summary
如果是二维相位去包裹问题,还有个奇点的问题。噪音、相位失真、奇点,似乎是所有相位解缠算法必须面对的三大问题。
相关Ipython Notebook文件和Einstein和Monalisa的图像在此下载
